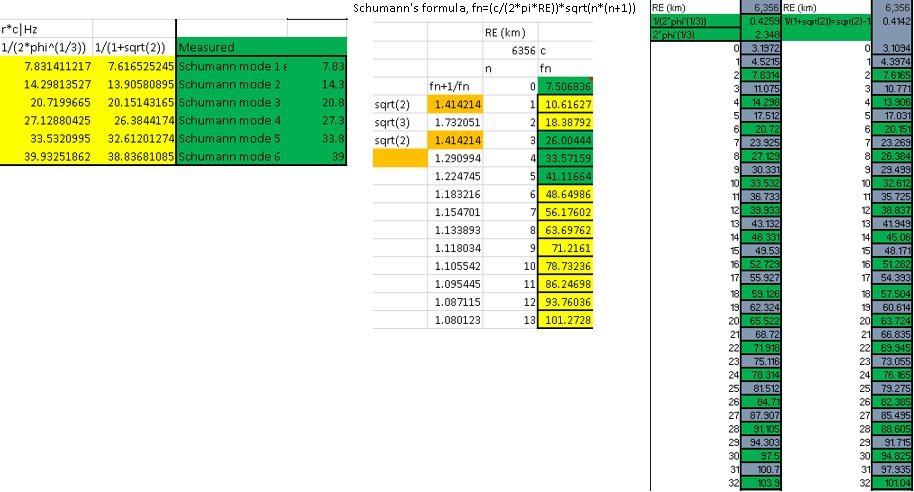
Nn+12 Formula Name

Solved 1 Pentagonal Numbers Name Exercise 11 1 Java A P Chegg Com

95 47 Sums Of Powers And Eulerian Numbers The Mathematical Gazette Cambridge Core

To Define Function And Introduce Operations On The Set Of Functions To Investigate Which Of The Field Properties Hold In The Set Of Functions Pdf Free Download

Reading And Writing Mathematical Proofs Spring 15 Lecture 2 Basic Proving Techniques Ppt Download

Contribution Of Indian Mathematicians Pdf Pi Mathematical Objects

Geometric Formulas Area Circle Free 30 Day Trial Scribd
1 plus 1 is 2, 2 divided by 2 is 1, 1 times 1 is 1.
Nn+12 formula name. But because you used the numbers twice, you only count 1/2 of them or (210)(421) is the total which is n/2(n+1) which rearranges to n(n+1)/2. This is the foundation for next few. 4 3 $\times$ 4 2 = ?.
Sum = 1 2 + 3 2 + 5 2 + 7 2 = 1 + 9 + 25 + 49 = 84 Input :. What Gauss did was think of this algebraically. X n = n(n+1)/2.
If you plug these numbers in you get:. So there are 6 possible combinations with 4 items. Let me write it over here.
The first element that you do is undo the superb element that were given tangled. Which is the same formula as before. The formula for the sum of the first n positive integers is n (n+1)/2.
Divide the sum by n-1. This formula works for consecutive integers. Since the numerator is a polynomial of degree 2 but the denominator is a polynomial of degree 3.
Figure – 7 :. Given a series 1 2 + 3 2 + 5 2 + 7 2 +. = (n+1) / (n+2) because we can cancel the common (n+1) factor from the numerator and denominator.
Take the square root to obtain the Standard Deviation. + (2*n – 1) 2, find sum of the series. T(n)+T(n) = i=n i i=1 + i=n (n+1–i) i=1 Two copies, one red and the other, reversed, in green2 T(n) = i=n (i +n+1–i) i=1 pair off the terms, a red with a green2 T(n) = i=n (n+1) i=1 n copies of (n+1):the i does not appear in the formula so all the terms are the same2 T(n) = n (n+1) T(n) = n (n+1) /2 The end.
Ardışık 2 tek doğal sayının çarpımı 195 ise toplamları kaçtır?. Johann Carl Friedrich Gauss is one of the most influential mathematicians in history. If observed closely, we can see that, if we take n common, series turns into an Harmonic Progression.
2^(2n) can be expressed as (2^n)(2^n), and 2^n isn't a constant. Sum of first n natural numbers - Derivation of a formula - Duration:. Now let's find a formula for this sum.
There are n of these (n+1)'s, so 2S n =n(n+1) So:. Also if not, what formula could I use?. It's the same thing as 2 plus n minus 1, which is the same thing as n plus 1.
S n =n(n+1)/2. A triangular number or triangle number counts objects arranged in an equilateral triangle (thus triangular numbers are a type of figurate numbers, other examples being square numbers and cube numbers). To sparkling up those variety of issues, get each and each of the letters on one area of the equation and the numbers on the different.
N = (-1 +- sqrt(1+8S))/(2) S = (n(n+1))/2 S = (n^2+n)/2 2S = n^2 +n n^2 + n - 2S = 0 using the quadratic formula for :. Notice that each column has a sum of n (not n+1, like before), since 0 and 9 are grouped. + n = (n(n+1))/2 Step.
#"using the method of "color(blue)"proof by induction"# #"this involves the following steps "# #• " prove true for some value, say n = 1"# #• " assume the result is true for n = k"#. Derivation of the formula in a way which is easy to understand. The second step is the inductive step.
(n / 2)(first number + last number) = sum, where n is the number of integers. Don’t stop learning now. N(n + 1)/2 = 1 3 6 10 15 Clearly the required sequence is double the one we have found the nth term for, therefore the nth term of the required sequence is 2n(n+1)/2 = n(n + 1).
The nth partial sum is given by a simple formula:. Start with the binomial expansion of (k. The first uses "" notation and the second introduces you to the Sigma notation which makes the proof more precise.
Imagine of the challenge like a knotted up ball of string. You need to show that if the statement is true for any particular value of n it is also true for the next value of n. There is a simple applet showing the essence of the inductive proof of this result.
The n th triangular number is the number of dots in the triangular arrangement with n dots on a side, and is equal to the sum of the n natural numbers from 1 to n. I’m assuming you mean math\frac{n(n+1)}{2}/math. No of parts ” n” = 4 so according to formula 4 x 5 /2 = 10.
You only need to sort n - 2 elements the second time through, n - 3 elements the third time, and so on. If it diverges. Sum = 1 2 + 3 2 + 5 2 + 7 2 + 9 2 + 11 2 + 13 2 + 15 2 + 17 2 + 19 2 = 1 + 9 + 24 + 49 +.
So 1 plus n is going to be n plus 1. The summation of an explicit sequence is denoted as a succession of additions. N N N-1 N-2.
Number of possible triangles in Fig – 8 = 15. The first is a visual one involving only the formula for the area of a rectangle. 2 plus n minus 1.
And now we can prove that this is the same thing as 1 times 1 plus 1 all of that over 2. This is called the variance. Ardışık sayıların toplamı gaus yönteminden n.(n+1)/2 den 11*12/2)=66 12a+66=318 12a=252 a=21 Soru:.
Ax^2 + bx + c = 0, n = (-b +- sqrt( b^2 - 4ac. Take 2 adjacent corners of the k sided figure and draw 2 sides from them. No of parts ” n” = 5 so according to formula 5 x 6 /2 = 15.
If it converges, nd the limit;. N = 10 Output :. We prove the formula 1+ 2+.
Now to add one more side to get k+1 sides, we do the following. Using the exponential formula (a m)(a n) = a m+n where a = 4 4 3 $\times$ 4 2 = 4 3+2 = 4 5 = 1024. And then we're going to add-- let me do it in pink-- 2 plus n minus 1.
Graph of Arithmetic, Geometric and Arithmetic-Geometric Progressions. Or to use the formula, (1/2) n, n being the number of total steps, times (n plus the fi. Finding n(n-1)/2 in the Real World Date:.
You need to find the number of steps, which is essentially the sum of all the steps in the staircase. Using the formula a 2 – b 2 = (a – b)(a + b) where a = 5 and b = 3 (a – b)(a + b) = (5 – 3)(5 + 3) = 2 $\times$ 8 = 16 Question 2:. Add those values up.
$2 \cdot T(n) = n(n+1) => T(n) = \frac{n(n+1)}{2}$ Triangular number just happen to arrange themselves in a simple pattern of an arithmetic progression of consecutive numbers. ∑ k = 1 n k = n ( n + 1 ) 2. Therefore, since 0 <1 the Ratio Test implies that the series converges.
Here number of parts ” n” then possible triangles is n (n+1) /2. Why divide by n-1 rather than n in the third step above?. (Noting that here, the number of terms is n-1) And to substitute the formula for the sum of a geometric series, into Equation 5.1 above:.
The son of peasant parents (both were illiterate), he developed a staggering. However, constant factors are the only thing you can pull out. Dots in triangle = n(n+1)/2.
Math, How can n(n-1)/2 be explained in common everyday language?. Figure – 8 :. So lets say we have 4 total items.
Now what I want to do is I want to assume that it works for some number k. Triangular series as n(n+1)/2, sequences of numbers. In a similar vein to the previous exercise, here is another way of deriving the formula for the sum of the first n n n positive integers.
Explain a formula Dear Dr. So this formula right over here, this expression it worked for 1, so we have proved our base case. That's the order of operations -- parentheses, exponents, multiplication.
+ 361 = 1330. Dots in rectangle = n(n+1) But remember we doubled the number of dots, so. Hello, I understand how to do it that way( I mean the way it's done in the picture send you) but how could I do it using the formula, n(n+1)/2 Is that the formula used for that question?.
We have proven it for 1. For example, summation of 1, 2, 4, 2 is denoted 1 + 2 + 4 + 2, and results in 9, that is, 1 + 2 + 4 + 2 = 9. (n+(1/2)) 2 = 961/4 We'll refer to this Equation as Eq.
It is a perfect square. We give three proofs here that the n-th Triangular number, 1+2+3++n is n(n+1)/2. Number of possible triangles in Fig – 7 = 10.
2n'den tek bir sayı çıkarılırsa tek bir sayı oluşur. Just multiply n by n+1. = lim n!1 (n+ 1)(n+ 2) (3n+ 3)(3n+ 2)(3n+ 1) = 0;.
1 2 3. 1 + 2 + 3 +. We can do this 6.
So what's 2 plus n minus 1?. + n = (n(n+1))/2 for n, n is a natural number Step 1:. \sum_{k=1}^n (2k-1) = 2\sum_{k=1}^n k - \sum_{k=1}^n 1 = 2\frac{n(n+1)}2.
= (n+1) 2 / ( (n+1)(n+2)) because we can factor the numerator now;. If you can do this then, since it is true for n = 1 it will also be true for the next value of n, n = 2. Because addition is associative and commutative, there is no need of parentheses, and the result is the same irrespective of the order of the summands.
If yes, then Carl Friedrich Gauss is the person you’re looking for. Start off with the case of n = 3 and verify that a triangle's 3 angles add up to 180. As you progress further into college math and physics, no matter where you turn, you will repeatedly run into the name Gauss.
{\displaystyle \sum _{k=1}^{n}k={\frac {n(n+1)}{2}}.} This equation was known to the Pythagoreans as early as the sixth century BCE. Get hold of all the important DSA concepts with the DSA Self Paced Course at a student-friendly price and become industry ready. (which means "that which was to be proven", in other words:.
#5.2.1 The Square Root Principle says that When two things are equal, their square roots are equal. Gauss was born on April 30, 1777 in a small German city north of the Harz mountains named Braunschweig. 11.Does the sequence arctan n2 n2 + 1 1 n=1 converge or diverge?.
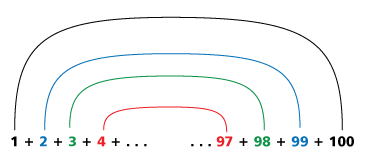
Thus you don't have to sort the whole thing every time:. Prove 1 + 2 + 3 +. Let's use the example of adding the numbers 1-100 to see how the formula works.
2 minus 1 is just 1. This is followed by two proofs using algebra. Thus the statement is true for n = 1.
So this is also going to be n plus 1. Look what happens if we write the first N integers in ascending order in one row, and then in descending order in the next row, and then add the numbers in each column:. Remember the trick, it is easier to remember than the formula.
The total of all the steps add up to 55. In step 1, you compute the difference between each value and the mean of those values. Red arrows flying in formation maths problem.
This is an arithmetic series, and the equation for the total number of times is (n - 1)*n / 2. Plz help me to solve do it step wise plz. Find the sum of the consecutive.
For the base case, you will probably want to start with n = 3 (i.e., when you have at least 3 elements in your set to begin with). That means that the total number of compare/swaps you have to do is (n - 1) + (n - 2) +. Now it is easy to work out how many dots:.
Bir sayısı çift bir sayıyla çarparsanız çift olur. And then this term over here. Space limitations require 0<n<11.Then push the Next button to step through the stages of the proof.
And instead of having exactly n items in 2 rows (for n/2 pairs total), we have n + 1 items in 2 rows (for (n + 1)/2 pairs total). It will also help student to remember the formula easily. We can use x n to mean "dots in triangle n", so we get the rule:.
(the given statement)\ Let P(n):. However, note that the formula agrees with the description when n = 0, 1, 2, as surely none of these sets have a 3-element subset. + n = n(n+1) / 2, for n.
Stack Exchange network consists of 176 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers. The ‘Gauss formula’ was thought to be invented in the late 1700’s, when Gauss was in elementary school. 09/14/02 at 10:33:49 From:.
Say you need to do ten steps. When is it used?. 1 --- --- --- --- N+1 N+1 N+1 N+1 Each column adds up to N+1.
Plugging 4 into the equation we get 4(4-1)/2 = 12/2 = 6. O(2^(n+1)) is the same as O(2 * 2^n), and you can always pull out constant factors, so it is the same as O(2^n). Applying the intuitive understanding of division as repeated subtraction, we can plot 12 on a numberline, and then since we are dividing by 2, we count backwards by 2 until we reach 0.
So, the answer to your questions are yes and no. Ie angles in a k-sided polygon sum to (k-2)*180. The right side is 2 n - 1= 2 1 - 1 = 1.
N = 4 Output :. Then assume the formula holds for some n = k.
Carboxylic Acid Reactivity
Q Tbn 3aand9gct9ujlz3opp Ivkhsmbzg8kjeufjwh0yh Osisnr Tg5qulmgs Usqp Cau

Program For Fibonacci Numbers Geeksforgeeks
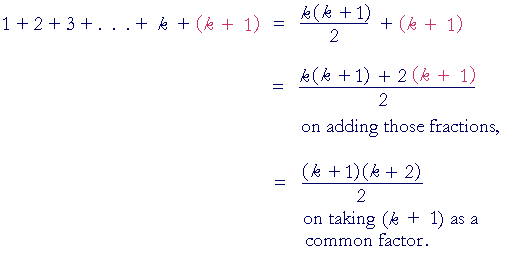
Mathematical Induction Topics In Precalculus

Hit23 ログイン ユーザ登録 高分子データベース Polyinfo Results2801 of23 Xml Xml Schema Xml Schema Help 検索キーワード Chlorine 同義語 Chlorine Cl 下のデータをクリックするとデータベースシステムのデータへ移動します

Solved A Check That The Following Formula 1 4 2 4 3 Chegg Com

Answers Compound Review

Mathematical Formula Tables
Faculty Math Illinois Edu Berndt Articles Koshliakov Pdf
Sum Of First N Natural Numbers Derivation Of A Formula Youtube

Csd Identifier Code Formula And Compound Name Of The Extracted Cif Download Table
Why Am I Not Able To Use Sn N 2 2a N 1 D Here But The Mark Scheme Uses N 2 A L The Student Room

By Rene Boyas Names Chemical Formula Is C 22 H 28 N 2 O Its Chemical Name Is N 1 2 Phenethyl 4 Piperidinyl N Phenyl Propanamide Like Heroin Morphine Ppt Download
2

175

Sequence Wikipedia
Www Certifico Com Component Attachments Download

175
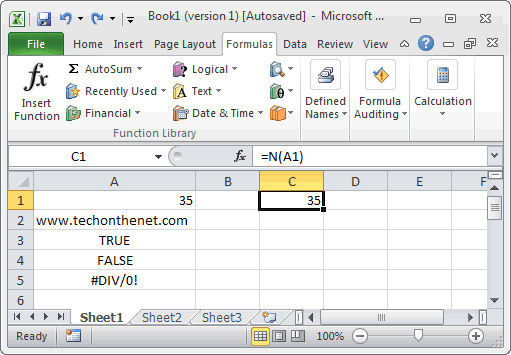
Ms Excel How To Use The N Function Ws

Given An Integer N It Is Required To Compute The Chegg Com

Solved Let N Be Geometric With Parameter 0 P 1 That Chegg Com

Python Functions Beginner To Expert By Srikanth Potukuchi Jul Medium

Intro To Arithmetic Sequences Algebra Video Khan Academy
Orphans Of Abductivism
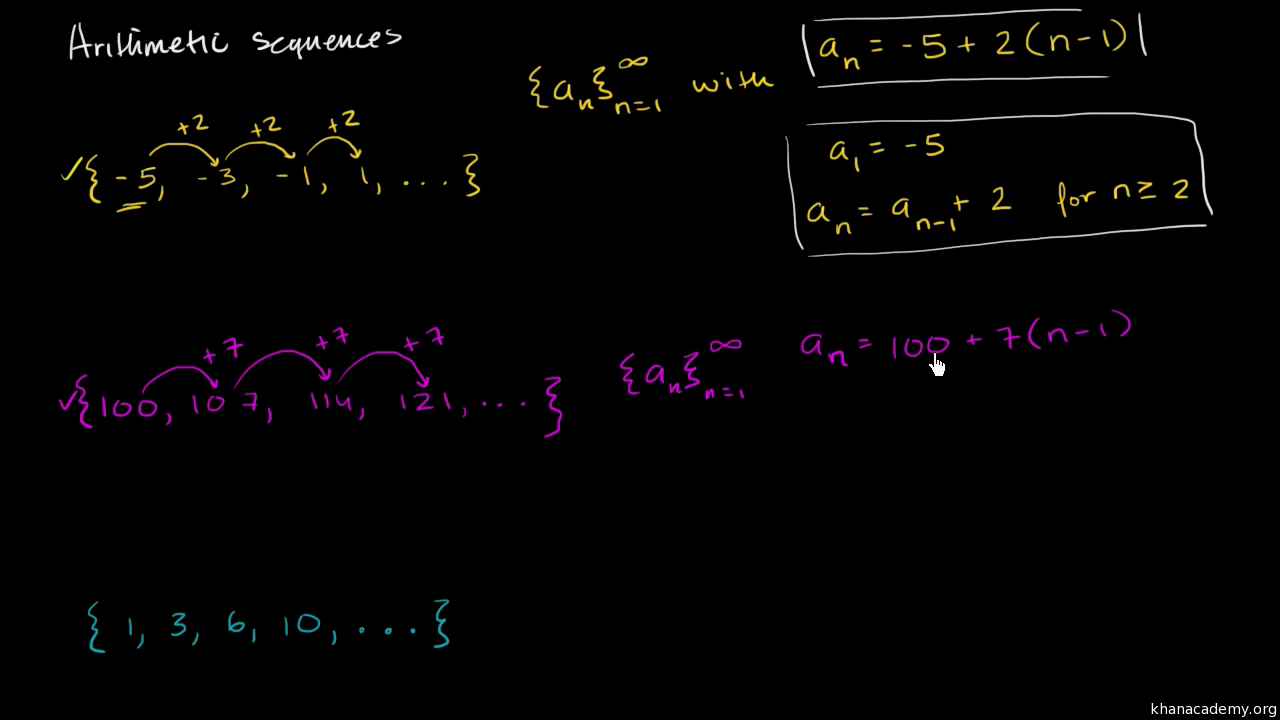
Intro To Arithmetic Sequences Algebra Video Khan Academy
/what-is-the-rydberg-formula-604285_final-251d1441e24e44c88aab687409554ed4.png)
What Is The Rydberg Formula And How Does It Work

Solved Weekly Homework 9 Math 132 Due Friday March 13 N Chegg Com

Infinite Series
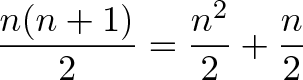
Techniques For Adding The Numbers 1 To 100 Betterexplained

Molecular Formula Molecular Name And Corresponding Abbreviation Of Download Table
Errors In Excel Types Examples How To Correct Errors In Excel

Key Section 2

Loops
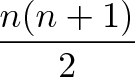
Techniques For Adding The Numbers 1 To 100 Betterexplained

Name Class Arithmetic Sequence Practice Which Context Best

7

Exam May 10 Spring 18 Questions Differential Equations Studocu

Mod 3 Lesson 1 Hw

Geometric Sequences And Sums

1 2 3 4 Wikipedia
Stirling S Approximation Wikipedia
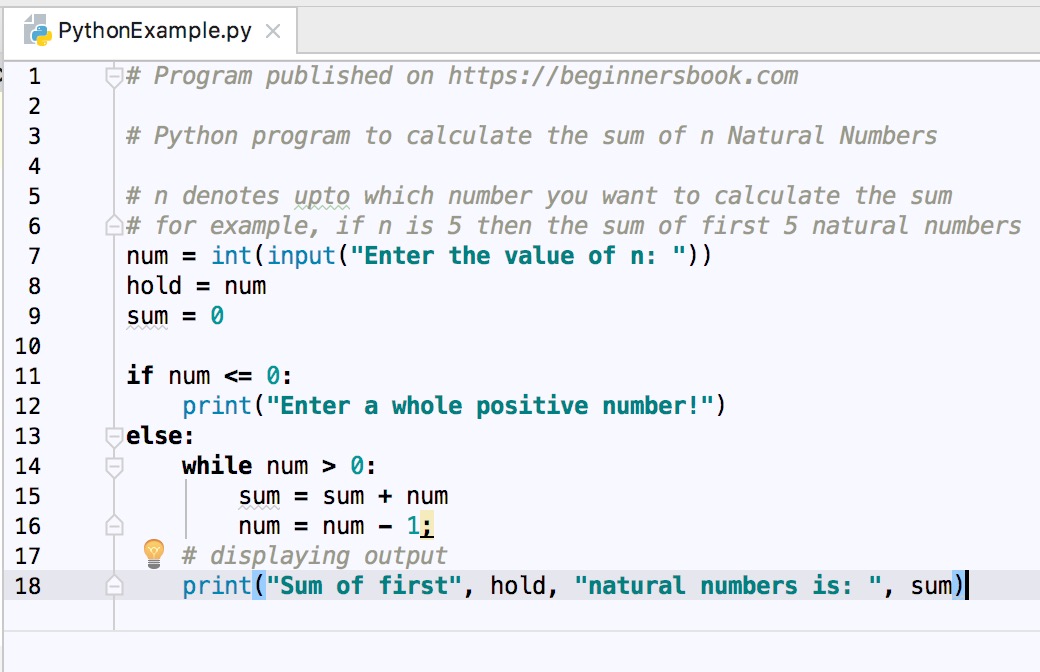
Python Program To Find Sum Of N Natural Numbers

Binomial Theorem

Ex 5 2 15 For What Value Of N Are Nth Terms Of Two Aps
Http Www Cabrillo Edu Hpayne Math 13 Lecture notes Chapter8 1 Filledout Pdf
Sequences Finding A Rule

Molecular Structures Iupac Name Smiles And Molecular Formula Of Download Scientific Diagram

Pascal S Triangle Wikipedia

Solved Binomial Coefficients You May Recall That The Bin Chegg Com

Tci America Trans N N Dimethylcyclohexane 1 2 Diamine D2946 1g 98 0 T Amazon Com Industrial Scientific

Pmp Formulas And Calculation For The Certification Demystified Project Management Business

Arithmetic Progression For Ssc Maths 14
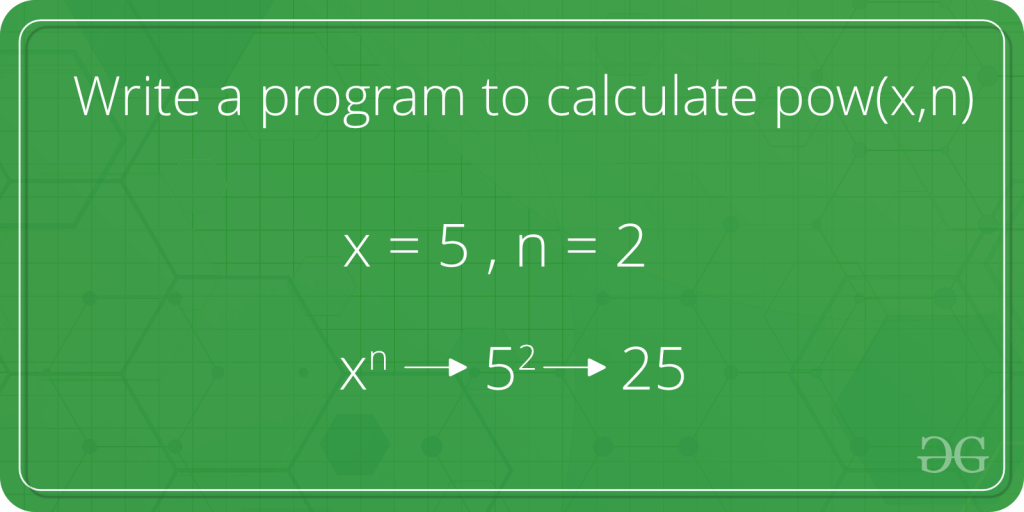
Write A Program To Calculate Pow X N Geeksforgeeks
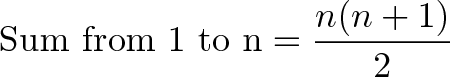
Techniques For Adding The Numbers 1 To 100 Betterexplained

Can Someone Help Me Answer Both A And B Please Name Laboratory Worksheet 8 Continued In Homeworklib

Compound Name And Molecular Formula With The Reference Code Used Download Table

Approximations For The Factorial Function

Arithmetic Progression Wikipedia

Solved Match Each Statistic S Name To Its Formula X I N Chegg Com
What Is The Name For The Pattern 1 2 4 8 16 What Is The Formula To Determine A Known Position In The Pattern Quora

356

Exam 1 Practice Test With Answers Math 1150 Clemson Studocu
2

Epb1 Resin System Google Patents
The Story Of Gauss National Council Of Teachers Of Mathematics

Formulas

Molecular Formula Molecular Name And Corresponding Abbreviation Of Download Table
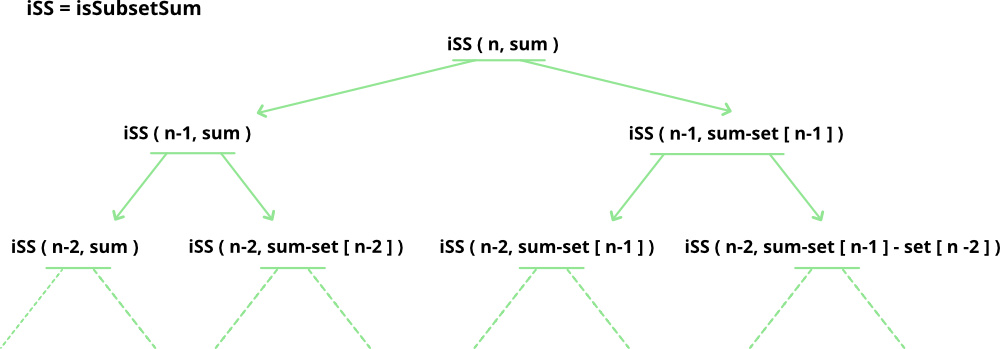
Dynamic Programming Subset Sum Problem

The Story Of Gauss National Council Of Teachers Of Mathematics

Math5700 Proof Homework Name Date

Discrete Mathematics Recursion And Sequences Ppt Video Online Download

List Of Math Formulas
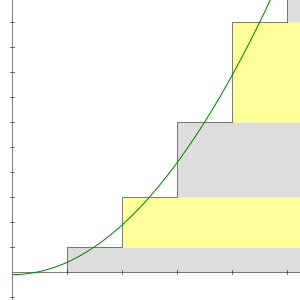
1 2 3 4 Wikipedia

Solved 1 Draw Condensed Or Expanded Structural Formula F Chegg Com

Solved Using This Homework As A Review For Our Quiz Later Chegg Com

Main C Notepad Homework 1 Solution 2 Msu Studocu

181

How To Find How Many Diagonals Are In A Polygon 11 Steps
Http Www Ketteringschools Org Userfiles 1142 Classes 1021 Algii03 05 12 Pdf

Factorial Wikipedia

Infinite Series
Q Tbn 3aand9gcsmwecr6dqmn8einfokyt8td2vhhbjzyf3hpfuqvhvt1qu07ryl Usqp Cau
Q Tbn 3aand9gcqlrwnub248bqau8ogje4 Hqvba A6vs6tvdlobpbwjwackwmta Usqp Cau

Solved 8 Let N Be Geometric With Parameter 0 P 1 Th Chegg Com

Combination Wikipedia

Combination Formula Video Combinations Khan Academy

Solved 1 Which Formula Name Combination Is Correct 5 00 Chegg Com
Q Tbn 3aand9gcqazg1klwwdkjxakshpnbz2jt2nnznxns2pmcq5hiueacursckb Usqp Cau

Nomenclature Packet 1 Name The Following Ionic Compounds A Al 2 O 3 Aluminum Oxide B Cs 2 O Cesium Oxide C Rb 3 N Rubidium Nitride Pdf Free Download

Ped Hsm11a2tr 08 1103 009

Sequences

Proof Of Finite Arithmetic Series Formula By Induction Video Khan Academy

The Connell Sum Sequence

181

How To Find How Many Diagonals Are In A Polygon 11 Steps

N 1 Phenylpropan 2 Yl Hydroxylamine N Hydroxyamph By Asch Issuu
Logarithm Rules Chilimath

Diagonal Of A Polygon Formula Diagonal Formula Byju S



