N2n+12 Habis Dibagi 4

Contoh Soal Induksi Matematika Habis Dibagi 2 Kumpulan Soal Pelajaran 5

52n 1 Habis Dibagi 5 Mas Dayat

Modul Logika Matematika
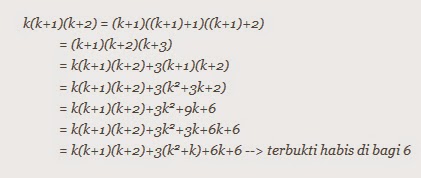
Buktikan N N 1 N 2 Habis Dibagi 6 Matematika Sup 2 Sup

Bank Soal Olimpiade Matematika

Soal Induksi
Apakah 74 habis dibagi 2?.

N2n+12 habis dibagi 4. Kita akan menunjukkan bahwa P(n) bernilai benar untuk semua bilangan bulat positif n. Definisi Bilangan Ganjil Bilangan ganjil adalah bilangan bulat positif yang tidak habis dibagi dengan angka \(2\). N (n +1) (n+2) = 1 ( 1+ 1 ) (1 + 2 ) = 1.
P(k+1) = 5(6 k) + 6 k + 4. 3 = 6 habis dibagi enam. Akan dibuktikan dengan P(n) benar pada masing-masing n ∈ N.
Sementara untuk bilangan yang habis dibagi 8. Maka 234 habis dibagi 6. N4 – 4n 2 habis dibagi 3 untuk n ≥2.
Misal n=3 (3+1) 2 <2(3) 2 16<18 Pernyataan benar untuk n=3. Dengan demikian (5 ^ k+1)-1 habis dibagi 4. 7^n-2^n habis dibagi 5.
Sebagai contoh, 4 habis dibagi 2 dan 6 habis dibagi 2, maka (4 + 6) juga habis dibagi 2. Sehingga P(k+1) dapat habis dibagi 5 dan pernyataan tersebut bernilai benar. Kuartil untuk jumlah data \((n)\) ganjil.
Rumus untuk bilangan genap adalah 2k untuk sebarang…. Buktikan 6 n + 4 habis dibagi 5, untuk masing-masing n bilangan asli. Karena 24 adalah kelipatan 4 atau bisa dibagi 4.
How to #12 Proof by induction 1^3+2^3+3^3++n^3= (n(n+1)/2)^2 n^2(n+1)^2/4 prove - Duration:. Ciri-ciri bilangan yang habis dibagi 4 adalah 2 angka terakhirnya habis dibagi 4. Jika disubstitusikan n=1 pada persamaan 7 n-2 n akan diperoleh 7 1-2 1 ,hasilnya = 5.
Harus memenuhi syarat bilangan habis dibagi 2 dan syarat bilangan habis dibagi 3. Domino yang pertama menyentuh. Dengan kata lain, syarat bilangan habis dibagi 6 adalah apabila digit-digitnya dijumlahkan harus habis dibagi 3 dan angkanya berakhiran 0, 2, 4, 6 dan 8.
Perhatikan 2 digit terakhir, di sana ada angka 24. Contoh Kata Pengantar Buku;. October 22, 19 Buktikan bahwa :.
Diperhatikan selisih p - s, p - s = x0 + x1101 + x2102 + … + xn10n - (x0 + x1 + x2 + … + xn) = (10 - 1)x1 + (102 - 1)x2 + … + (10n - 1)xn Diperhatikan bilangan pada ruas kanan selalu habis dibagi sembilan, misalnya ditulis 9m untuk suatu bilangan bulat m. Kuartil untuk banyaknya data \((n)\) genap dan tidak habis dibagi 4. 8^n - 1 habis dibagi 7 untuk setiap bilangan asli b.
Kita tahu 5 habis dibagi 5. Segera ditunjukkan P(1) benar 6 1 + 4 = 10 habis dibagi 5. 6 n + 4 habis dibagi 5, untuk n bilangan asli.
Untuk setiap nilai n, k, dan k+1 dari 4ⁿ+¹ - 4 selalu TERBUKTI. Akan ditunjukkan bahwa 5n − 1 juga habis dibagi 4 untuk n = k + 1, yaitu 5k+1 − 1 habis dibagi 4. * BILANGAN HABIS DIBAGI 2 Suatu bilangan habis dibagi 2, ciri-cirinya adalah bilangan yang berakhiran (berangka satuan) 0, 2, 4, 6, 8.
Berapapun nilai \(k\) selama dia bilangan bulat positif, ketika dikalikan dengan \(2\) pasti akan habis dibagi dua, alias sisanya nol. Jika p habis dibagi a dan q habis dibagi a, maka (p + q) juga habis dibagi a. Maka bilangan tersebut habis dibagi 4.
4.Buktikan dengan induksi matematika bahwa untuk setiap bilangan asli n, 72n+1 +1 habis dibagi oleh 8. N^4 – 4n^2 habis dibagi 3, untuk semua bilangan bulat lebih dari sama dengan 2 Posted on:. Sehingga syarat bilangan habis dibagi 6.
Yang sangat jelas habis dibagi 4. Suatu string biner panjangnya n bit. Jumlah semua digitnya habis dibagi 3.
(n=2)= 2 3 +3.2 2 +5.2+3 = 8+12+10+3 = 33 è kelipatan 3 è 10 Contoh 3 :. Langkah Basis Induksi, Untuk n=2 , maka. 2n > n 2 untuk n>4.
Apakah 74 habis dibagi 2?. Soal Induksi Buktikan :. E) 4 2 n −4 n habis dibagi 3 untuk Jawab :.
Min mohon penjelasan lebih dalam dong ,bagaimana si bisa di rubah menjadi +3(K+1)(K+2). 213.324.064 habis dibagi 8 karena 3 digit akhir - 064 dan ini habis dibagi 8. Hasilnya =0, angka 0 dibagi 3 adalah 0;.
Karena langkah dasar dan langkah induktif terbukti, maka dapat disimpulkan bahwa 5^n-1 dapat dibagi 4 untuk setiap n=bilangan positif. Akan menunjukan P(1) benar 6 1 + 4 = 10 habis dibagi 5. Buktikan bahwa untuk setiap bilangan bulat positif n,.
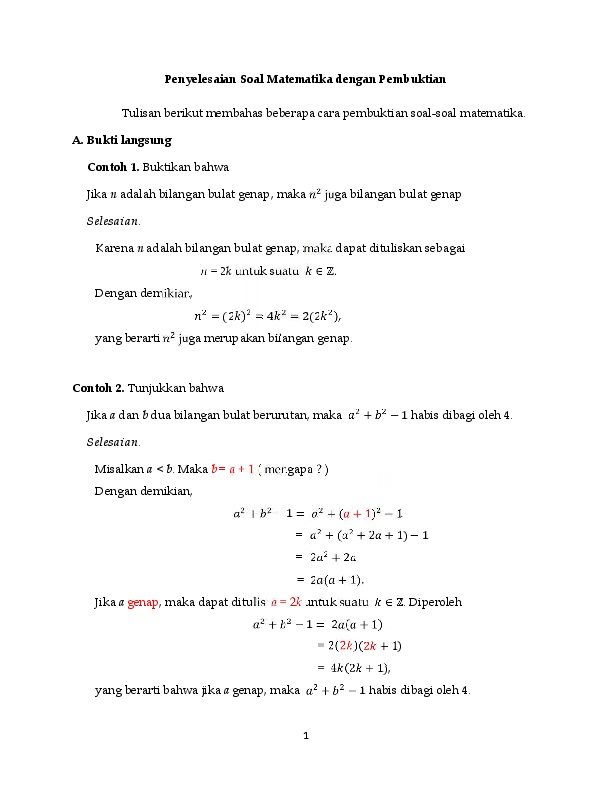
Merupan bentuk bilangan ganjil, jadi terbukti bahwa \(n^{2}\) bilangan ganjil. Induksi Matematika merupakan salah satu metode pembuktian dalam matematika, selain Induksi Matematika ada beberapa metode lain yang biasa digunakan dalam pembuktian kebenaran suatu pernyataan seperti pembuktian langsung, pembuktian tak lanngsung, trivial, dan sebagainya. Soal dan Pembahasan – Induksi Matematika pada Deret dan Ketaksamaan Soal juga tersedia dalam format PDF yang dapat diunduh melalui tautan berikut:.
SOAL JAWAB INDUKSI MATEMATIKA #HABIS DIBAGI 5 - Duration:. Jadi kesimpulannya terbukti bahwa n(n+1)(n+2) habis dibagi 6 semoga jawaban ane membantu gan. Dengan demikian, bilangan berbentuk 7n 2n dapat dibagi oleh 5 untuk setiap n.
6 k + 4 habis dibagi 5, k ∈ N. Dengan menggabungkan hasil pada langkah pembuktian 1 dan 2. Asumsikan bahwa 5n 1 habis dibagi 4 untuk n = k, yaitu 5k 1 habis dibagi 4.
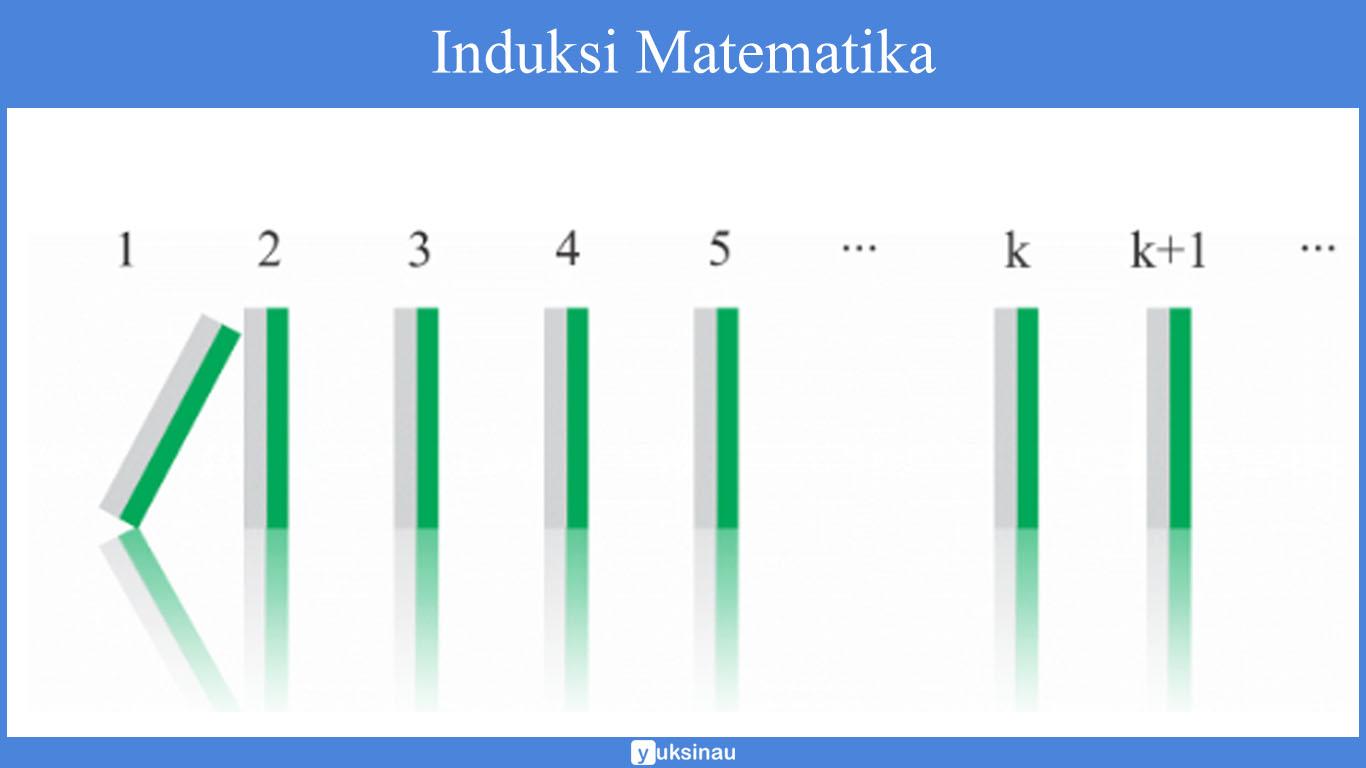
N-4n^2 habis dibagi 3 untuk semua n bilangan bulat, n>atau samadengan 2!. Dengan kata lain bilangan itu adalah bilangan genap. Cara yang paling gampang untuk mengetahui bagaiman prinsip kerja induksi matematika yaitu dengan cara mengamati efek domino.
Jika semua bilangan bulat positif n, 3 pangkat 2n ditambahkan dengan 2 pangkat 2n + 2 akan habis dibagi dengan angka 5, buktikan dengan induksi matematika!. 5.Buktikan dengan induksi matematika bahwa untuk setiap bilangan asli n, 2 4n+3 +3 3n+1 habis dibagi oleh 11. Karena 74 merupakan bilangan….
6 x 7^n - 2 x 3^n habis dibagi 4 untuk setiap n bilangan asli. 4n < 2 n, untuk masing-masing bilangan asli n ≥ 4. Jadi, pernyataan "10 habis dibagi 5" dapat kita tulis menjadi "10 = 5m, untuk m bilangan bulat" Berdasarkan konsep diatas, pembuktian keterbagian dapat pula diselesaikan dengan cara sebagai berikut.
Gunakan induksi matematis untuk membuktikan bahwa n 3 – n dapat dibagi dengan 3 apabila n adalah suatu bilangan bulat positif. Contohnya gini deh, \(6\) habis dibagi \(2\) dan \(10\) habis dibagi \(2\), maka \((6 + 10)\) juga habis dibagi \(2\). By Fina Dhea Posted on 29/12/19.
Artinya untuk n= 1, benar. Akan ditunjukkan bahwa 5n 1 habis dibagi 4 untuk n = 1. Bisa juga dikatakan bahwa bilangan habis dibagi 6 adalah bilangan.
Next Posting Lebih Baru Previous Posting Lama. Berdasarkan induksi matematika yang dilakukan menunjukkan bahwa pernyataan “6 n + 4 habis dibagi dengan 5, untuk setiap n adalah bilangan asli” adalah benar. Buktikan untuk setiap bilangan asli n ≥ 2 berlaku.
Download (PDF, 87 KB). Bentuk 5(6 k) dapat habis dibagi 5 dan bentuk 6 k + 4 juga habis dibagi dengan 5. Untuk jumlah data yang kecil, penentuan kuartil lebih mudah ditentukan dengan piramida berikut ini.
Misalkan pernyataan benar untuk n=k (k+1) 2 <2k 2. Oke inilah dia contoh soal induksi matematika bentuk pembagian. View 1ef.docx from BUSINESS MISC at Erusmus University Rotterdam.
Akan kita tunjukkan 5 k + 1 – 1 juga habis dibagi 4. Ibaratkan bahwa P(k) benar, yakni:. Karena pernyataan memuat syarat n≥3 maka langkah pertama pembuktian menggunakan n=3, bukan n=1 seperti yang digunakan sebelumnya.
Akan ditunjukkan bahwa 5n − 1 habis dibagi 4 untuk n = 1. Definisi “habis dibagi” sudah aku jelasin di tulisan sebelumnya, cek aja yaa. Prinsip, Pembuktian Deret, Keterbagian, Persamaan dan Contoh Soal – Apakah itu Induksi Matematika ?Pada kesempatan kali ini Seputarpengetahuan.co.id akan membahas tentang Bola Kasti beserta hal-hal yang melingkupinya.
Karena jumlah angka-angkanya habis dibagi 3 dan bilangan itu genap. 2n 1 untuk setiap n = 1;2;:::. Soal Induksi Matematika, Buktikan :.
Langkah Induksi, untuk n +1, maka = n 4 – 4n 2 = (n+1) 4 – 4(n+1) 2 = n 4 +4n 3 +6n 2 +4n+1 – 4(n 2 +2n+1) = n 4 + 4n 3 + 6n 2 + 4n + 1 – 4n 2 – 8n – 4. Khusus bagi siswa SMA yang ingin belajar online serasa offline bisa klik no wa berikut https://wa.wizard.id/1efd69. Jumlah string biner yang mempunyai bit 1.
Jadi terbukti bahwa n(n + 1)(n + 2) habis dibagi 3 untuk n bilangan asli 08. Langkah pertama buktikan P (1) benar. Buktikan 4^n+1 - 4 habis dibagi 12 - Jawab:.
Jika n adalah bilangan bulat positif maka n(n+1) adalah bilangan genap. Rumus-rumus di atas sangat baik digunakan untuk jumlah data banyak. 2) Berikutnya untuk n=k, di asumsikan benar.
Pelajari materi dan contoh soal induksi matematika di sini. Jadi, () benar untuk 3 adalah faktor − untuk semua bilangan bulat positif n karena memenuhi kedua langkah pembuktian Buktikan bahwa − habis dibagi 4 untuk semua bilangan bulat positif n!. Keterbagian C.1 Uji habis dibagi Ciri-ciri bilangan yang habis dibagi n.
Jadi, 7 k-2 k habis dibagi 5 atau agar lebih mudah bisa ditulis menjadi 7 n-2 n = 5a, a Є bilangan asli. Pada tahun $01$, seorang fisikawan dari Exploratorium San Fransisco, melakukan eksperimen dengan membuat keping domino dari kayu lapis sebanyak $8$ keping, masing-masing $50\%$ lebih besar dari keping sebelumnya.Keping yang pertama ukurannya $5$ cm, keping yang kedua ukurannya $7,5$ cm. N 4 – 4n 2 habis dibagi 3, untuk semua bilangan bulat lebih >=2.
Carilah rumus umum dari 1^3 =1, 2^3 = 3 + 5, 3^3 = 7+9+11, 4^3 = 13 +15 + 17 + 19 Kemudian buktikan dengan induksi matematika. Pembahasan Misalkan P(n) adalah pernyataan 1 + 2 + 3 + … + n = n(n + 1)/2. Untuk membuktikan kasus ini maka kita mesti tahu bahwa bilangan kelipatan 100 pasti habis dibagi 4 (sebab 100 juga hais dibagi 4).
Baca Juga Bilangan Asli dan Cara Menghitungnya. Kita anggap 5 k – 1 habis dibagi 4 untuk sebarang bilangan bulat positif k. Kita harus menunjukkan bahwa P(1) benar.
Jelas sekali bahwa 51 1 = 5 1 = 4 habis dibagi 4. 2 + 4 + 6 + … + 2n = n(n + 1), n bilangan asli P(n):. 4 dapat habis dibagi 2 dan 6 dapat habis dibagi 2, Sehingga (4 + 6) juga dapat habis dibagi 2.
Jadi, kita dapat menyimpulkan bahwa 5 n – 1 habis dibagi 4 untuk semua bilangan bulat positif n. Merupakan perkalian tiga bilangan berurutan, seperti:. Karena 74 merupakan bilangan genap (Ingat rumus untuk bilangan genap.
3 7n 1 2n 1 7.7 n 7.2 n 7.2 n 2.2 n = 77 n 2n 5.2 n = 7(5m) + 5.2n m N (asumsi P n benar) = 5(7m + 2n) Karena 7m + 2n bilangan asli, maka dari kesamaan terakhir kita dapat menyim-pulkan bahwa 7n 1 2n 1dapat dibagi dengan 5.Dengan kata lain, pernyataan P n+1 adalah benar. Berdasar asumsi , (5 ^ k)-1 habis dibagi4. Buktikan bahwa (n+1) 2 <2n 2 untuk setiap n≥3 dan n anggota bilangan asli.
Akan dilihat 3 digit angka, apakah 3 digit tersebut bisa dibagi8 atau tidak. Jika x dan y bilangan bulat maka (x^n - y^n) habis dibagi (x-y) untuk setiap n bilangan asli. Habis dibagi Ciri-ciri Contoh 2 Digit terakhir genap 9736, , dst 3 Jumlah digit-digitnya habis dibagi 3 57 = 5 + 7 = 12 4 Dua digit terakhir habis dibagi 4 5 Digit terakhir 0 atau 5 7235 6 Habis dibagi 2 dan 3 = 4 + 1 + 8 + 7 + 4 =24, genap dan.
Berikut sifat-sifat pertidaksamaan yang sering digunakan:. Sekarang kita perhatikan jumlah angka-angkanya. + a^n = (1- a^n+1) / ( 1 –a) untuk semua n >=0 dan a tidak sama dengan 1.
11 n – 6 habis dibagi 5 untuk n ≥1. Karena 4 ∙ 5 k dan 5 k – 1 habis dibagi 4 maka 5 k + 1 – 1 habis dibagi 4. Contoh Buktikan jika 6 n + 4 habis dibagi 5, untuk tiap n merupakan bilangan asli.
Soal-soal berikut merupakan soal tentang induksi matematika yang berhubungan dengan keterbagian bilangan. Sedangkan 4.(5 ^ k) juga habis dibagi 4. Karena p habis dibagi 9 maka dapat ditulis p = 9k untuk suatu bilangan bulat k.
Untuk membuktikan pernyataan tersebut benar, maka akan. 6 n + 4 habis dibagi 5. Kita akan buktikan bahwa Basis Induksi n=2 , => Untuk n=3 , => Untuk 4 n ≥2 2 n.
N 4 – 4n 2 = 2 4 – 4.2 2 =16 – 16 = 0;. Anda dapat menyatakan bahwa 2+4+6+…+2n=n(n+1) adalah benar. Ada contoh mengenai keterbagian dan pertidaksamaan.
N ( n + 1) ( n + 2) habis dibagi 6. Asumsikan bahwa 5n − 1 habis dibagi 4 untuk n = k, yaitu 5k − 1 habis dibagi 4. Kita juga bisa mengatakan bahwa jika bilangan habis dibagi ab, maka bilangan itu habis dibagi a dan habis dibagi b.
Jelas sekali bahwa 51 − 1 = 5 − 1 = 4 habis dibagi 4. Untuk soal induksi yang berhubungan dengan deret dan ketaksamaan bilangan, silakan kunjungi tautan di bawah. Tunjukan bahwa banyaknya himpunan bagian dari suatu himpunan yang mempunyai anggota sejumlah n adalah 2 n.
Efek domino tidak hanya berlaku untuk keping-keping yang sama besarnya. 524 habis dibagi 4 sebab 24 habis dibagi 4. Materi Pembinaan Menuju OSN Matematika 132SMA DARUL ULUM 2 JOMBANG/DIDIK SADIANTO, S.Pd.Contoh 1:Buktikan bahwa jika habis dibagi 3 maka n habis dibagi 3.Pembahasan:Kita akan membuktikan pernyataan ini dengan metode tidak langsung.Yakni kita harus membuktikan pernyataan jika n tidak habis dibagi 3 maka n2tidakhabis dibagi 3.Perhatikan bahwa.
Kuartil untuk banyaknya data \((n)\) genap dan habis dibagi 4. Contoh 1.2 Gunakan induksi matematika untuk membuktikan bahwa 5n 1 dapat dibagi 4 untuk setiap n = 1;2;:::. Dengan kata lain bilangan itu adalah bilangan genap.
5k+1 − 1 = = = =. 638 tidak habis dibagi 4 sebab 38 tidak habis dibagi 4. 6 n + 4 dapat habis dibagi 5 Maka segera dibuktikan P(n) benar untuk tiap n ∈ N.
Buktikanlah bahwa untuk n ≥ 4 dan n bilangan asli berlaku 3 n > n 3 Jawab Ambil n = 4 maka 3 4 > 4 3 artinya 81 > 64 (bernilai benar) Ambil n = 5 maka 3 5 > 5 3 artinya 243 > 125 (bernilai benar) Ambil n = 6 maka. 1x2x3, 2x3x4, 3x4x5, , (n-3)(n-2)(n-1), n(n+1)(n+2), dll. Sebagai contoh, "10 habis dibagi 5" benar karena terdapat bilangan bulat m = 2 sehingga 10 = 5.2.

Pengertian Rumus Dan Contoh Soal Induksi Matematika Ruang Les Online

Induksi Matematika Nelly Indriani Widiastuti Teknik Informatika Unikom Ppt Download

Modul 1 Bilangan Bulat

5 2n 1 Habis Dibagi 5 Brainly Co Id

Ppt Induksi Matematika
Induksi Matematika Materi Lengkap Matematika

Buktikan Dengan Induksi Matematika Bahwa 2 Pangkat 2n 1 1 Habis Dibagi 3 Brainly Co Id

25 Soal Dan Pembahasan Induksi Matematika Pendidikan Matematika Laman 5

25 Soal Dan Pembahasan Induksi Matematika Pendidikan Matematika Laman 5
Induksi Matematika Materi Lengkap Matematika

Buktikan N N 1 N 2 Habis Dibagi 3 Induksi Matematika Bagian 6 Youtube

Contoh Soal Induksi Matematika Habis Dibagi Brainly Kumpulan Soal Pelajaran 5

Induksi Matematika Makalah Prinsip Dan Contoh Soal

Contoh Soal Induksi Matematika Habis Dibagi 2 Kumpulan Soal Pelajaran 5

Induksi Matematika Habis Dibagi 4 Youtube

Fakultas Sains Dan Teknologi Ppt Download

Soal Induksi Mtk Dan Cara Penyelesaian Mtk Smansa Aul

Induksi Matematika

Induksi Matematika Materi Contoh Soal Pembuktian

2 1 Pendahuluan 2 2 Keterbagian

Buktikan Secara Indukdi Bahwa 11 Pangkat N 6 Habis Dibagi 5 Untuk N Semua Bilangan Asli Brainly Co Id

Soal Dan Pembahasan Induksi Matematika Sumber Soal Buku Siswa Matematika Sma Kurikulum 13 Defantri Com
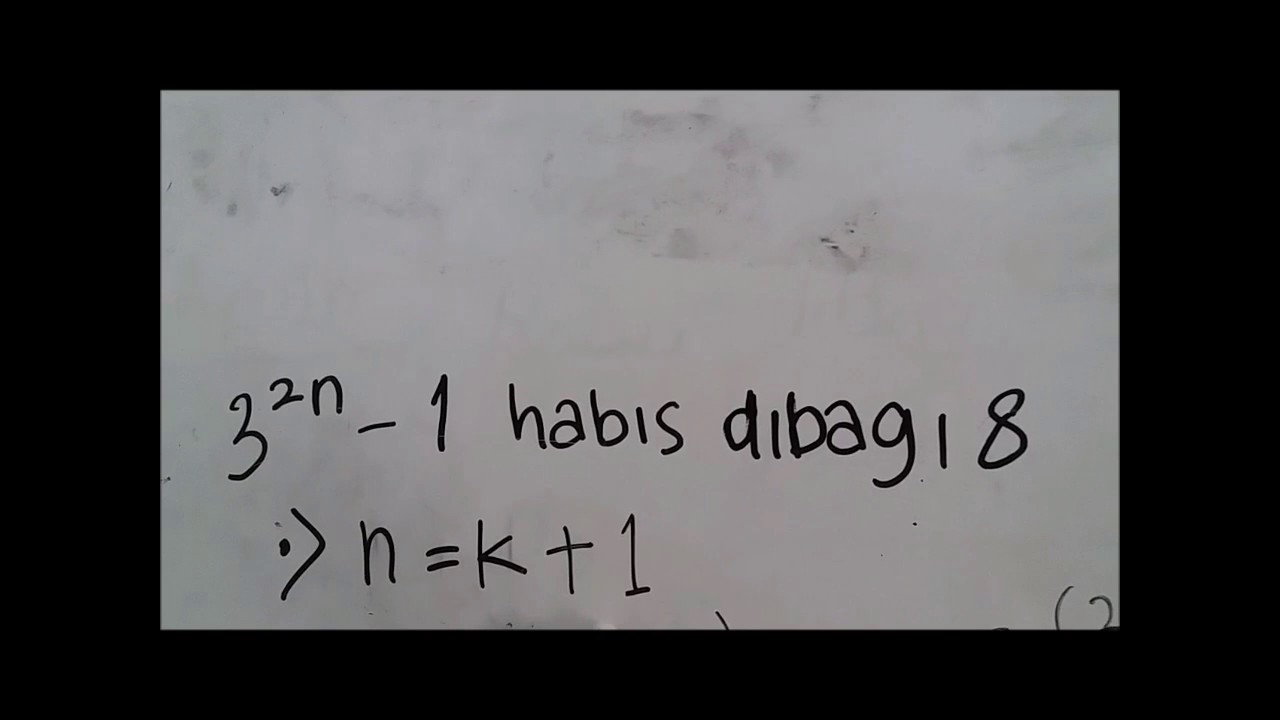
Contoh Soal Induksi Matematika Youtube

Pdf Soal Soal Olimpiade Matematika Dan Penyelesaiannya Ary Brainer Academia Edu

Induksi Matematika Prinsip Pembuktian Deret Keterb

Dengan Induksi Matematika Buktikan Bahwa 5ⁿ 1 Habis Dibagi 4 Brainly Co Id

Doc Kumpulan Soal Jawab Olimpiade Matematikadaripertemuan Berau Putri Utiw Academia Edu
Induksi Matematika Materi Lengkap Matematika

Soal Jawab Induksi Matematika Habis Dibagi 3 Youtube

Soal Induksi

Buktikan Bahwa N Pangkat 3 N Habis Dibagi 3 N Lebih Besar Sama Dengan 2 Brainly Co Id

Contoh Soal Induksi Matematika Habis Dibagi 2 Kumpulan Soal Pelajaran 5

Induksi Matematika

Matematika Wajib Kelas Xi Ips

Tolong Bantu Ya 7 2n 1 3 2n Habis Dibagi 8 Brainly Co Id

Contoh Soal Induksi Matematika
Induksi Matematika Materi Lengkap Matematika
Induksi Matematika Materi Contoh Soal Pembuktian

Contoh Soal Induksi Matematika Habis Dibagi 2 Kumpulan Soal Pelajaran 5

Bilangan Habis Dibagi Docx

Teori Bilangan

Soal Latihan Induksi Matematika

Soal Dan Pembahasan Induksi Matematika Sumber Soal Buku Siswa Matematika Sma Kurikulum 13 Defantri Com

人気ダウンロード Nn 1n 2 Habis Dibagi 6

Bab 3 Prinsip Inklusi Eksklusi

Logika Matematika Bab 5 Induksi Matematika Ppt Download

Sbmptn Flip Book Pages 101 150 Pubhtml5

Bab I Induksi Matematik Induksi Matematik Merupakan Salah

Buktikan Dengan Induksi Matematika Bahwa A 2n 1 B 2n 1 Habis Dibagi Oleh A B Untuk Semua Bilangan Brainly Co Id

Buktikan Bahwa N Pangkat 3 N Habis Dibagi 3 N Lebih Besar Sama Dengan 2 Youtube

Doc Soal Jawab Kuis4 Alya Putri Academia Edu

Part I College Mudah Dengan Induksi Matematika Bahwa Untuk Setiap Bilangan Asli N 72n 1 1 Habis Dibagi

Induksi Matematika Ppt Download

Cari Bilangan Yang Jika Ditambah 0 1 2 3 4 5 6 Berturut Turut Habis Dibagi 2 3 4 5 6 7 8 Youtube
Contoh Soal Induksi Matematika Habis Dibagi 2 Kumpulan Soal Pelajaran 5

Bank Soal Olimpiade Matematika
Http Informatika Stei Itb Ac Id Rinaldi Munir Matdis 03 04 Unlicensed Soaljawabkuis4 Pdf

Soal Induksi

25 Soal Dan Pembahasan Induksi Matematika Pendidikan Matematika Laman 5

Fakultas Sains Dan Teknologi Ppt Download

Induksi Matematikabuktikan6 7 N 2 3 N Habis Dibagi 4 Brainly Co Id

Induksi Matematika 6x7 N 2x3 N Habis Dibagi 4 Youtube

Modul 1 Bilangan Bulat

Prinsip Inklusi Eksklusi

Buktikan Bahwa 7 Pangkat N 2 Pangkat N Habis Dibagi 5 Untuk Setiap N Elemen Bilangan Asli Brainly Co Id
Soal Jawab Induksi Matematika Habis Dibagi 5 Youtube

Dengan Induksi Matematika 5n 3n Habis Dibagi Mas Dayat
Induksi Matematika Materi Lengkap Matematika

25 Soal Dan Pembahasan Induksi Matematika Pendidikan Matematika Laman 7

Buktikan N N Habis Dibagi 3 Untuk Setiap N Bilangan Asli Brainly Co Id

Kelas 11 Sma Matematika Siswa 17 Pages 1 50 Text Version Anyflip

Pengertian Rumus Dan Contoh Soal Induksi Matematika Ruang Les Online

25 Soal Dan Pembahasan Induksi Matematika Pendidikan Matematika Laman 5

Jumlah Bilangan Bulat Antara 10 Dan 100 Yang Habis Dibagi 3 Tetapi Tidak Habis Dibagi 5 Adalah Youtube

Induksi Matematika Buktikan Bahwa 11 N 6 Habis Dibagi 5 Untuk N Bilangan Asli Youtube

25 Soal Dan Pembahasan Induksi Matematika Pendidikan Matematika Laman 5

Buktikan Bahwa 5pangkat N 1 Habis Dibagi 4 Untuk Setiap N Adalah Anggota Asli Brainly Co Id
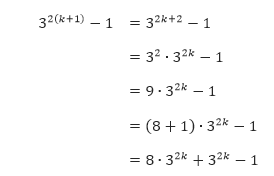
25 Soal Dan Pembahasan Induksi Matematika Pendidikan Matematika Laman 5

Induksi Matematika

Kumpulan Soal Jawab Olimpiade Matematika

Uh Induksi Matematika 17 18
Pdf Penyelesaian Soal Matematika Dengan Pembuktian Kusuma Hadi Purnawan Academia Edu

Induksi Matematika 6x7 N 2x3 N Habis Dibagi 4 Youtube

Contoh Soal Induksi Matematika Habis Dibagi 2 Kumpulan Soal Pelajaran 5

Induksi Matematika E Learning Kelas 22 29 Desember Ppt Download

25 Soal Dan Pembahasan Induksi Matematika Pendidikan Matematika Laman 5

Contoh Soal Induksi Matematika

Contoh Soal Induksi Matematika Habis Dibagi 2 Kumpulan Soal Pelajaran 5

Jumlah Seluruh Bilangan Asli Antara 1 100 Yang Habis Dibagi 3 Tetapi Tidak Habis Dibagi 5 Adalah Youtube

Gunakan Induksi Matematika Untuk Menunjukan Bahwa 5n 1 Habis Dibagi 4 Untuk Semua Bilangan Bulat Brainly Co Id

Dari Soal Di Bawah Ini Buktikan Bahwa 1 1 2 3 N N N 1 Adalah Benar Untuk Setiap Brainly Co Id

Buktikan Dengan Induksi Matematika Bahwa 5 N 1 Habis Dibagi 4 Untuk Semua Bilangan Positif N Brainly Co Id

Contoh Soal Induksi Matematika Habis Dibagi Brainly Kumpulan Soal Pelajaran 5

Materi Dasar Teori Bilangan 1



